Software Diagnostics and Observability Institute

Introduction

Models of the world are traditionally evaluated by their ability to predict observable outcomes. Accuracy, likelihood, loss functions, and benchmark scores dominate both scientific and engineering practice. Yet such criteria say little about how a model organizes reality, how stable its explanations are under perturbation, or how it changes as systems evolve. In long-lived software systems, diagnostic pipelines, simulators, and modern AI models, these questions become central. What is required is a framework for comparing models not merely by performance, but by structure. We propose a framework that treats model comparison as a topological diagnostic problem, building on the previous ideas and earlier work on software defects, causal models, geometrical debugging, models of software behavior, higher-order pattern narratives, topological software trace and log analysis, traces and logs as models of computation, and pattern-oriented observability.

World Models as Topological Mappings

At the foundation of this approach lies a simple abstraction. Any model of the world may be understood as a mapping f_i: W → M_i, where W denotes a space of world states, observations, executions, traces, or narratives, and M_i denotes the internal representational space of the model, including latent variables, symbolic explanations, diagnoses, predictions, or narratives produced by the model. The crucial assumption is that both W and M_i are not mere sets, but spaces equipped with topology, that is, with a notion of neighborhood and nearness. This assumption is deliberately weak. It does not require metrics, probabilities, or differentiability, yet it is strong enough to speak meaningfully about continuity, deformation, invariants, and discontinuities.

Software as a World

In this framework, software systems themselves may be treated as worlds rather than merely as artifacts within a world. A running software system defines its own space of states, executions, interactions, and narratives, shaped by control flow, data flow, concurrency, configuration, and environmental inputs. From the perspective of diagnostics and observability, this space is not secondary or derivative; it is the primary reality with which engineers interact. Crashes, performance anomalies, security violations, and semantic failures occur within this software world, even when they have no immediate counterpart in the physical environment. Treating software as a world enables the direct application of topological reasoning to execution behavior, traces, and models, without requiring an appeal to external “ground truth.” The world W is thus not restricted to physical systems or user-visible outcomes, but includes the internally generated realities of computation itself. This perspective underlies treating traces, logs, and models as world models: they are successive representations of a world that is already artificial, structured, and designed.

Traces as First-Class World Models

Execution traces and logs are often treated as neutral records of system behavior, positioned between the world and higher-level analytical models. In practice, however, traces and logs already function as world models in their own right. They are selective, structured, and interpretive representations of execution, shaped by instrumentation choices, logging schemas, sampling strategies, and storage constraints. As such, they impose structure on reality before any further analysis takes place.

Formally, tracing introduces a mapping f_trace∶ W → T, from the space of executions W to a trace or log space T. This mapping is neither complete nor transparent. It encodes decisions about which events matter, how time is represented, how causality is inferred, and which invariants are preserved or discarded. Consequently, traces do not merely expose the world; they actively model it.

Recognizing traces as first-class world models has important diagnostic consequences. Continuity, homotopy, invariants, and discontinuities apply at the trace level just as they do at the level of analytical models. Discontinuities may arise not from changes in execution, but from changes in instrumentation, log formatting, sampling, or correlation mechanisms. Similarly, two tracing systems may produce structurally different traces that are nevertheless homotopic, preserving diagnostic meaning despite representational variation.

This perspective also clarifies the composition of diagnostic models. Analytical world models operate not directly on execution, but on trace-based representations. The effective mapping from the world to a model is therefore a composition of mappings, W →^f_trace T →^f_model M, and failures of observability may originate at any stage in this chain. Treating traces as first-class world models allows diagnostic reasoning to localize such failures precisely, distinguishing system faults from tracing artefacts and modeling defects.

By elevating traces and logs to the status of world models, observability itself becomes a modeling problem rather than a purely instrumental one. The quality of diagnosis depends not only on the sophistication of analytical models, but on the structural faithfulness of the trace models on which they are built. In this sense, trace design is model design, and tracing infrastructure becomes an integral part of the diagnostic and epistemic foundation of complex systems.

Continuity as a Diagnostic Criterion

Under this abstraction, a model is no longer merely a function producing outputs, but a structural interpreter of the world. Comparing models, therefore, means comparing how they preserve or distort the neighborhood structure of W. Continuity becomes the first diagnostic criterion. A model is continuous if small perturbations in the world induce only local changes in the model’s internal representation. When two models are compared, the model that preserves neighborhoods more faithfully is structurally superior, even if both achieve comparable accuracy on test data. Continuity violations manifest operationally as brittle behavior, unstable explanations, excessive sensitivity to noise, adversarial fragility, or abrupt diagnostic jumps.

Homotopy and Model Equivalence

Continuity alone is insufficient to capture deeper notions of model equivalence. Two models may differ substantially in implementation, architecture, or parameterization, yet encode the same understanding of the world. This motivates treating homotopy as an equivalence relation up to deformation. Two models f₁,f₂: W → M are homotopic if there exists a continuous deformation H: W × [0,1] → M such that H(w,0)=f₁(w) and H(w,1)=f₂(w). Homotopy captures the idea that one model can be transformed into another without tearing, collapsing, or introducing new discontinuities. When such a homotopy exists, the models differ representationally but not conceptually. When no such homotopy exists, the difference is not cosmetic: the models carve the world differently. This notion generalizes the Trace Homotopy analysis pattern from execution traces to world models, preserving endpoints and invariants while allowing internal variation.

Invariants and Semantic Anchors

A further dimension of comparison arises from invariants. Certain structures are expected to remain unchanged under valid modelling transformations. These may include causal ordering, temporal directionality, conservation-like quantities, semantic identities, protocol structure, or the persistence of specific message components across executions. In Pattern-Oriented Diagnostics, this idea is formalized in the Message Invariant trace and log analysis pattern. Empirically, trace messages emitted from the same source code fragment typically contain invariant parts, such as function names and symbolic descriptions, alongside mutable parts, such as pointer values, object identifiers, version numbers, or error codes. By separating invariant structure from variable content, diagnosticians can isolate semantically meaningful differences while suppressing incidental variation.

When lifted to the level of world models, invariants act as semantic anchors. A model may preserve topological continuity while violating message invariants, thereby maintaining neighborhood structure but destroying meaning. Conversely, a model that rigidly enforces invariants while distorting continuity risks suppressing legitimate variation. Invariant preservation, therefore, defines what must remain fixed for two representations to be models of the same world.

Discontinuities as Diagnostic Signals

Discontinuities occupy a central place in this diagnostic perspective and are directly linked to the Discontinuity trace and log analysis pattern. In trace and log analysis, discontinuities appear as abrupt changes in execution flow, unexpected gaps, reordered sequences, missing segments, or sudden shifts in narrative vocabulary. Such events often mark fault boundaries, regime changes, configuration transitions, version mismatches, or failures of observation itself.

The same insight applies at the level of world models. When a model introduces a discontinuity in the mapping f: W → M, it implicitly claims that the world itself undergoes a meaningful transition at that point. The diagnostic question, therefore, is whether this transition corresponds to a genuine break in execution narratives or is merely a model-induced tear. Unaligned discontinuities signal structural mismatch between the model and the world, whereas aligned discontinuities often correspond to real events.

Structural Translation Between Models

The strongest form of model comparison arises when one asks whether models can be translated into one another in a structurally faithful way. Suppose there exists a mapping T: M₁ → M₂ such that f₂ ≈ T ∘ f₁. If this diagram commutes up to isomorphism and the translation preserves continuity and invariants, then the two models are structurally equivalent and differ only in representation. If no such translation exists, the disagreement is fundamental: the models impose incompatible organizations on the world.

Models as Diagnostic Artefacts

Viewed through the lens of Pattern-Oriented Diagnostics, models themselves become diagnostic artefacts. They can be inspected, compared, versioned, and classified using the same structural reasoning traditionally applied to traces, logs, and memory dumps. Model comparison thus becomes an exercise in identifying continuity violations, invariant breaks, homotopy obstructions, and unexplained discontinuities, rather than merely ranking predictive performance.

Engineering World Models for Observability

Observability has traditionally been treated as a property of systems rather than of models. Logs, traces, metrics, and signals are collected around a system, and diagnostic reasoning is applied externally to infer what the system is doing and why. In this view, models are consumers of observability data or predictors built on top of it, but not themselves objects of observability. As models increasingly mediate understanding, explanation, and control of complex systems, this separation between models and observability becomes untenable. Engineering the models for observability requires a fundamental inversion: observability must become a property of the model itself.

When a model is engineered for observability, it is no longer sufficient for it to produce accurate predictions. The model must preserve the diagnostic structure of the world and make it inspectable. If the model is understood as a mapping f: W → M, from a space of world states, executions, or observations to an internal representational space, then engineering for observability means designing this mapping so that distinctions, transitions, and invariants in the world remain visible within the model. Understanding is no longer reconstructed after the fact; the model’s structure carries it.

At the foundation of observable models lies continuity. An observable model is continuous by default: small changes in the world induce small, traceable changes in the model’s internal state. This property is essential for diagnosis because, in the absence of continuity, there is no reliable basis for comparison. Noise becomes indistinguishable from events, and explanations jump unpredictably across regimes. Continuity provides a baseline against which deviations can be detected and interpreted. In this sense, continuity is not a mathematical refinement but a prerequisite for trustworthy observability.

Continuity alone, however, is insufficient. Real systems undergo genuine transitions, failures, and regime changes, and an observable model must make such events explicit. This requires engineering for controlled discontinuity. Rather than allowing arbitrary or emergent breaks in behavior, an observable model introduces discontinuities deliberately, at semantically meaningful boundaries. These discontinuities preserve identifiable pre- and post-states and can be aligned with discontinuities observed in traces, logs, or execution narratives. When discontinuities are engineered in this way, they become diagnostic events rather than opaque failures. When they are not, they manifest as model-induced tears that obscure rather than reveal system behavior.

Observability also extends across time, versions, and evolution. Models are retrained, refactored, or replaced, yet diagnostic understanding must persist across these changes. Engineering the models for observability, therefore, requires homotopy: the ability to relate different versions of a model through continuous deformation. When successive models are homotopic, representational changes do not destroy meaning. Diagnostic baselines remain comparable, explanations evolve smoothly, and understanding accumulates rather than resets. Without homotopy, every model update becomes an epistemic rupture, forcing diagnostics to start from scratch.

Another essential aspect of observability is the preservation of invariants. Observable models must retain stable semantic anchors that survive across executions and contexts. These include conceptual identifiers, protocol meanings, narrative roles, and other invariant structures that define what remains the same when everything else varies. This requirement generalizes message-level invariants from trace and log analysis to the level of models themselves. A model may preserve continuity yet violate invariants, producing internally smooth behavior that silently destroys meaning. Conversely, a model that enforces invariants rigidly while distorting continuity suppresses legitimate variation. Engineering for observability requires balancing continuity and invariance so that both structure and meaning remain accessible.

A deeply observable model also supports partial reversibility. While full inversion of the world model mapping is neither possible nor necessary, an observable model allows diagnostic backtracking. From an explanation, one can infer a class of world states; from an anomaly, one can identify a structural cause; from an output, one can locate an internal regime. This partial reversibility enables diagnostic reasoning to flow not only forward, from world to model, but also backward, from model behavior to plausible world structure.

Taken together, these properties define a clear design principle. A model is engineered for observability if its internal structure preserves the diagnostic patterns present in the world and makes violations of those patterns explicit, localized, and interpretable. This principle is stronger than interpretability and orthogonal to accuracy. A model may be accurate yet unobservable, just as it may be interpretable yet diagnostically opaque.

The consequences of engineering models for observability are substantial. Failures become explainable rather than mysterious; diagnostics remain stable across versions; anomalies acquire structural meaning; and long-lived systems accumulate understanding rather than lose it. Most importantly, the model itself becomes part of the observability stack rather than merely a consumer of signals. Observability is no longer something added around a model; it is something the model embodies.

From this perspective, engineering the models for observability is not an optional refinement but a necessary response to the increasing role models play in shaping how complex systems are understood, diagnosed, and trusted.

Related Work

The ideas developed here intersect with several established bodies of work, including topological methods in data analysis, semantic models in software engineering, research on robustness and interpretability in machine learning, and observability in complex systems. At the same time, they differ from these traditions in both emphasis and scope, treating world models themselves as diagnostic artefacts and grounding their comparison and observability explicitly in Pattern-Oriented Diagnostics.

Topological concepts have long been used in the analysis of physical systems, dynamical systems, and, more recently, in data analysis through techniques such as topological data analysis and manifold learning. In these contexts, topology is typically applied either to the underlying system under study or to the geometry of the observed data. Continuity, connectedness, and invariants are used to reason about stability, phase transitions, or qualitative structure. By contrast, we apply topological reasoning not directly to data or physical state spaces, but to the mapping induced by a model. The object of analysis is not the world alone, but the relationship between the world and its representation inside a model, and, crucially, how this relationship affects what can be observed, interpreted, and diagnosed through the model.

In machine learning, related concerns appear under the headings of robustness, generalization, adversarial stability, and representation learning. Many approaches implicitly assume continuity by enforcing smoothness, imposing Lipschitz constraints, or regularizing latent spaces. Other work studies model sensitivity and brittleness through perturbation analysis. However, such approaches typically remain metric- or loss-driven and focus on performance degradation rather than structural interpretation. Observability, when discussed, is often reduced to logging activations, inspecting attention maps, or probing internal representations post hoc. The framework presented here reframes robustness and sensitivity as topological properties of the world–model mapping, making discontinuities, folds, and violations of invariance first-class diagnostic and observability signals rather than secondary effects of optimization.

Interpretability and explainability research also overlap conceptually with this work. Post hoc explanation methods, concept-based explanations, and symbolic abstractions aim to render model behavior understandable to humans. While valuable, these techniques often operate locally or retrospectively. The present approach instead emphasizes structural faithfulness and structural observability: whether a model preserves neighborhood relations, semantic invariants, and execution narratives globally and across versions. In this sense, the work aligns more closely with epistemic notions of model validity and observability than with visualization or explanation alone.

In software engineering and systems diagnostics, traces, logs, metrics, and execution narratives have long been treated as primary artefacts for observability and diagnostics. Pattern-Oriented Diagnostics, including patterns such as Discontinuity, Trace Homotopy, and Message Invariant, provide a vocabulary for reasoning about stability, change, and failure in observed system behavior. Prior work in this area has focused on concrete execution artefacts and observability signals emitted by running systems. The present contribution extends this diagnostic and observability reasoning to models themselves, treating them as higher-order artefacts that can be inspected, compared, and classified using the same structural principles. In this view, models are not merely consumers of observability data but participants in the observability stack.

The notion of homotopy used here is inspired by both classical topology and its diagnostic analogue in trace analysis. In execution traces, homotopy captures equivalence between different internal paths that preserve endpoints and invariants, enabling observability across execution variability. By lifting this idea to world models, the paper introduces a principled way to distinguish representational change from conceptual drift, and to maintain observability across model evolution, retraining, and refactoring. While homotopy has occasionally appeared as a metaphor in machine learning discourse, we use it systematically as a model comparison and observability criterion grounded in diagnostic practice.

Finally, the idea of invariant preservation connects this work to formal methods, protocol verification, and contract-based design, where invariants play a central role. However, those approaches typically treat invariants as hard constraints or correctness conditions. In contrast, the diagnostic perspective adopted here treats invariant violations as observability signals to be interpreted, localized, and explained, rather than simply as failures. This positions invariant reasoning within observability and diagnosis rather than within verification alone.

In summary, we synthesize mathematical and conceptual components drawn from well-established traditions into a Pattern-Oriented Diagnostics framework for world models that explicitly incorporates observability as a structural property. The unification of topological reasoning, diagnostic patterns, and engineered observability lies at the intersection of systems diagnostics, AI model evaluation, and epistemic analysis of complex systems.

Conclusion

World models should be treated as diagnostic artefacts whose structure, stability, and evolution can be examined using the same principles applied to execution traces, logs, and memory dumps. By adopting a topological perspective, models are understood as mappings between spaces of observations and internal representations, allowing continuity, homotopy, invariants, and discontinuities to serve as principled criteria for comparison and diagnosis.

Within this framework, continuity characterizes epistemic robustness, homotopy distinguishes representational change from conceptual drift, message invariants anchor semantic commitments, and discontinuities become interpretable signals rather than mere errors. Established trace and log analysis patterns, such as Discontinuity, Trace Homotopy, and Message Invariant, generalize naturally to the level of models, providing a direct bridge between concrete diagnostic practice and abstract model evaluation. These same properties also define model-level observability, ensuring that internal model states, transitions, and explanations remain traceable, comparable, and diagnostically meaningful.

The resulting shift is conceptual as much as technical. Model evaluation moves away from narrow performance-centric criteria toward questions of structural faithfulness: where a model preserves neighborhood structure, where it introduces tears, which invariants it respects, and which changes correspond to real transitions in the world rather than artefacts of modelling. In an era of long-lived software systems, complex observability pipelines, and increasingly opaque AI models, such questions are no longer optional.

From the perspective of Pattern-Oriented Diagnostics, models themselves become first-class subjects of diagnosis. A good model is one whose topology changes only when the world itself changes, whose invariants break only when semantic commitments change, and whose discontinuities correspond to genuine events rather than modelling artefacts. Topological comparison, therefore, complements traditional evaluation by restoring structure, meaning, and interpretability to the practice of modelling complex systems.

Appendix

Case Study: Diagnosing Model Evolution in a Distributed Order Processing System

This case study illustrates how continuity, homotopy, message invariants, and discontinuities jointly support diagnostic reasoning across system behavior and model evolution. The example is drawn from a distributed order-processing system, whose execution traces are used both for operational diagnosis and for training and validating a world model that predicts and explains system behavior.

System Context

The system consists of an order service, a pricing component, a payment gateway, and a persistence layer. Execution traces are collected across multiple deployments and model versions. A world model f: W → M is constructed to map observed executions to internal representations that capture causal structure, service interactions, and outcome states. Over time, the system undergoes minor configuration changes, internal refactoring, and a major incident, providing a natural setting in which all four diagnostic concepts arise.

Continuity: Stable Behavior Under Small Perturbations

Under normal operation, the system processes orders with slight variations in input parameters, such as order amount or user identifier. Traces collected during this phase exhibit stable structure: the same services are invoked in the same order, and the same outcome is produced. Only numeric parameters and identifiers differ.
From the perspective of the world model, these executions correspond to nearby points in the world space W that are mapped to nearby representations in M. The mapping is continuous: small changes in input lead to small, localized changes in representation. This continuity establishes a baseline of epistemic stability. It allows the diagnostician to interpret deviations meaningfully, knowing that the model does not amplify noise into structural change.

Homotopy: Representational Change Without Conceptual Drift

The authentication subsystem is later refactored to improve performance. The refactoring alters the internal order of validation and profile-loading steps but preserves all externally observable semantics. Traces before and after the refactoring differ in internal sequencing but share the same start conditions, invariants, and outcomes.

These trace families are homotopic. There exists a continuous deformation from the pre-refactoring mapping f₀ to the post-refactoring mapping f₁ such that, for each execution, intermediate representations preserve identity, authorization outcome, and security constraints. The world model reflects this by allowing a smooth deformation of its internal structure while maintaining semantic anchors. Diagnostic understanding is preserved across versions: the model evolves without conceptual drift.

Message Invariants: Anchoring Semantic Comparison

During routine comparative analysis across users, a discrepancy in object-creation behavior was detected. Trace messages emitted from the same code location contain invariant components, such as function names and symbolic descriptors, alongside variable components, such as object addresses and version numbers. The invariant message structure enables direct comparison across executions.

By isolating invariant parts, diagnosticians identify that a particular user’s trace consistently references a different object version than all others. This difference is semantically meaningful rather than incidental. In the world model, these invariants correspond to fixed semantic anchors that must be preserved across mappings. The violation indicates a divergence in interpretation for a specific subset of world states, prompting further investigation.

Discontinuity: Structural Rupture and Diagnostic Event

A production incident occurs following a configuration update. Traces that previously exhibited stable cache behavior suddenly show cache eviction followed by a null reference failure. The transition is abrupt: new execution paths appear without a gradual lead-up, and previously invariant assumptions are violated.

This event constitutes a discontinuity. In trace space, it appears as a sudden change in structure. In the world-model mapping, it manifests as a jump that cannot be explained by continuous deformation. The model implicitly asserts that the world has undergone a significant transition. The diagnostic analysis confirms that the configuration update introduced an incompatible cache policy. The discontinuity is aligned with a real-world event rather than being a modelling artefact.

Integrated Diagnostic Interpretation

Viewed in isolation, each of these phenomena is familiar to engineers. Viewed together, they form a coherent diagnostic narrative. Continuity establishes a stable interpretive baseline. Homotopy allows representational change without loss of meaning across evolution. Message invariants anchor semantic comparison and expose subtle divergences. Discontinuities signal genuine regime changes requiring explanation.

Crucially, the same concepts apply at both the trace and model levels. The world model is not merely trained on traces; it is itself subject to diagnosis using the same structural principles. Its continuity, homotopy, invariance under transformations, and discontinuities determine whether it remains a faithful, observable representation of the system.

Implications

This case study demonstrates that the proposed topological framework is operationally meaningful. It unifies routine trace analysis and higher-level model evaluation within a single diagnostic vocabulary. By engineering models that preserve continuity, admit homotopy, respect invariants, and expose discontinuities, diagnostic understanding can accumulate over the course of system evolution rather than being repeatedly reset. In this sense, the model becomes a first-class diagnostic artefact and an integral component of the observability stack.

Case Study: Diagnosing a Faulty World–Model Mapping

This case study examines a scenario in which observed execution behavior remains stable, yet diagnostic failures arise due to defects in the world-model mapping itself. Unlike the previous case, in which discontinuities reflected genuine system events, the present example demonstrates that the model can violate continuity, homotopy, and invariants even when the underlying system remains well-behaved.

System Context

The same distributed order processing system is operating under stable production conditions. Execution traces collected over time exhibit consistent structure, ordering, and outcomes. No configuration changes, refactoring, or incidents occur during the observation window. A world model f: W → M is trained to map execution traces into an internal representation used for anomaly detection and root-cause analysis.

A new version of the model is introduced after retraining with additional data and a modified representation layer. Shortly after deployment, the model begins reporting anomalous regime changes despite the absence of corresponding changes in the execution traces.

Apparent Discontinuity Without Trace Evidence

The model flags abrupt transitions between internal states corresponding to “normal operation” and “degraded performance.” These transitions appear as sharp jumps in the model’s internal space, triggering alerts and diagnostic workflows. However, a review of the underlying traces reveals no corresponding discontinuities. Message ordering, component interactions, and outcomes remain consistent with historical baselines.

From a topological perspective, this discrepancy is immediately significant. The mapping from the world to traces is continuous, whereas the mapping from traces to the model is not. The latter mapping introduces a discontinuity that is not present in the world. This indicates a model-induced tear rather than a world event.

Failure of Homotopy Across Model Versions
Further investigation compares the previous model version f₀ with the newly deployed version f₁. Although both models are trained on overlapping data and intended to represent the same system semantics, no continuous deformation exists that relates f₀ to f₁ while preserving invariants. Small variations in traces that previously produced small representational changes now result in qualitatively different internal states.

The absence of a homotopy between f₀ and f₁ indicates conceptual drift introduced by the model rather than by the system. The models are not merely different implementations; they impose incompatible organizations on the same world.

Invariant Violation in the Representation

Inspection of the internal representations reveals that certain semantic anchors previously preserved by the model have been lost. Messages that were formerly mapped to stable conceptual identifiers are now distributed across multiple internal categories based on incidental parameters, such as timing or identifier ranges. Message-level invariants present in the traces are no longer preserved in the model representation.

This violation is subtle. The traces themselves still contain invariant structure, but the mapping fails to respect it. As a result, semantically identical executions are interpreted as distinct, fragmenting the diagnostic narrative. The failure is not one of observability instrumentation, but of representational fidelity.

Continuity Breakdown as a Mapping Defect

The combined effect of these changes is a breakdown of continuity in the world-model mapping. Nearby points in the world space, nearly identical executions, are mapped to distant regions in the model space. The model amplifies insignificant variation into structural differences. This violates the baseline assumption required for meaningful diagnosis: that small causes produce small effects in representation.

Importantly, this breakdown occurs without any corresponding trace-level instability. Continuity holds in the world and in the observability artefacts, but fails in the model.

Diagnostic Resolution

Recognizing the issue as a mapping fault rather than a system fault reframes the diagnostic task. Instead of searching for hidden incidents or race conditions, attention shifts to the model’s design and training process. Analysis reveals that a normalization change in the representation layer introduced a sharp boundary condition, effectively partitioning the model space in a way that has no counterpart in the world.

The corrective action is therefore model-centric: restoring invariant preservation, smoothing the representation, and re-establishing continuity and homotopy with the prior model version. Once these properties are restored, spurious anomalies disappear without altering the underlying system.

Implications

This case study demonstrates the diagnostic power of treating models themselves as artefacts subject to topological analysis. By comparing continuity, homotopy, and invariant preservation across traces and models, it becomes possible to distinguish genuine world events from representational artefacts. Discontinuities that arise in the absence of trace-level evidence can be correctly attributed to the mapping rather than the system.

Case Study: Diagnosing Failure Across a Hierarchy of World Models

This case study examines a production incident in which execution traces and logs serve as an intermediate world model linking system behavior to higher-level analytical models. The example demonstrates how continuity, homotopy, message invariants, and discontinuities must be evaluated not only between the world and a model, but across a hierarchy of models. The failure ultimately happens neither in the system nor in the analytical model, but in the trace model itself.

System and Observability Context

Consider a distributed payment processing system comprising an API gateway, an authorization service, a fraud-detection component, and a payment provider. Execution traces and logs are collected using a centralized tracing infrastructure that emits structured logs with correlation identifiers. These traces serve as the primary input to a diagnostic world model f_model∶ T → M, where T denotes the trace space and M an internal representation used for anomaly detection and causal analysis.

Implicitly, tracing itself defines a prior mapping f_trace∶ W → T, from actual executions in the world W to observable traces.

Continuity at the Trace Level

Under normal operation, small variations in user behavior, such as transaction amounts or geographic locations, produce traces with a stable structure. The same services are invoked, messages appear in consistent order, and outcomes are unchanged. Minor parameter differences are reflected only in message payloads.

At the trace level, the continuity holds: nearby executions in W map to nearby traces in T. The analytical model f_model further preserves this continuity, mapping these traces to nearby internal states in M. Diagnostic baselines remain stable, and no anomalies are reported.

Homotopy Across Trace Schemas

To reduce log volume, the tracing team deploys a new version of the logging schema. Some messages are merged, others reordered, and verbosity is reduced. Despite these changes, semantic anchors, such a transaction identifiers, authorization outcomes, and service boundaries, are preserved.

Although the resulting traces differ structurally from earlier ones, they are homotopic with respect to diagnostic meaning. There exists a deformation between the old trace mapping f⁽⁰⁾_trace and the new mapping f⁽¹⁾_trace that preserves endpoints and invariants. Experienced diagnosticians can still interpret the traces correctly, and the analytical model continues to function as expected. Observability across trace evolution is preserved.

Message Invariants as Trace-Model Commitments

Within the trace model, certain message components function as invariants: correlation IDs, service names, and outcome labels. These invariants anchor meaning across executions and across schema versions. The analytical model relies on them to group events, infer causality, and detect deviations.

At this stage, invariant preservation holds at both levels: the system produces consistent behavior, and the trace model faithfully preserves its semantic structure.

Discontinuity Introduced by the Trace Model

A subsequent optimization introduces aggressive sampling in the tracing infrastructure. Under high load, certain internal service calls are no longer logged, and correlation identifiers are omitted for sampled-out spans. No changes are made to the system itself.

From the system’s perspective, behavior remains continuous. However, the trace mapping f_trace now introduces a discontinuity. Traces that were previously structurally similar suddenly lack key messages and identifiers. From the viewpoint of the analytical model, executions appear to jump abruptly between unrelated internal states.

The model flags severe anomalies: apparent partial executions, missing authorization steps, and unexplained failures. Yet inspection of raw system metrics and business outcomes reveals no corresponding incident. The discontinuity exists only in the trace space.

Diagnostic Localization Across the Model Hierarchy

Applying the framework proposed in this paper, diagnosticians analyze continuity and invariants across the composed mapping W →^f_trace T →^f_model M. They observe that continuity holds in W, fails in T, and is amplified in M. Homotopy between trace versions is broken: no deformation preserves diagnostic meaning after sampling removes invariant components. The analytical model is behaving correctly with respect to its input; the failure lies in the trace model.

Corrective action is therefore taken at the level of observability, not at the level of system logic or model architecture. Sampling policies are revised to preserve invariant messages and correlation structure. Once this is done, continuity is restored in T, homotopy with prior traces re-emerges, and spurious anomalies disappear from M.

Integrated Interpretation

This case study demonstrates that traces and logs are not passive artefacts, but active world models whose structure directly determines what higher-level models can observe and infer. Continuity, homotopy, invariants, and discontinuities must be evaluated across all layers of representation. A failure at any layer can manifest as a diagnostic anomaly, even when the underlying system is stable.

By treating traces as first-class world models, the diagnostic process can correctly attribute failures to their source. In this case, the problem was neither a system fault nor a modeling defect, but a breakdown in the trace-world mapping. Recognizing this distinction prevents misdirected remediation efforts and reinforces the central claim of this work: effective observability and diagnosis depend on the structural faithfulness of every model in the representational hierarchy.

These examples complete the diagnostic picture. Failures may originate either in the world or in the models. The proposed framework provides tools for distinction. In doing so, it reinforces the central claim: that observability and diagnosis depend as much on the structure of the mapping as on the behavior of the system being observed.

PDF: https://www.dumpanalysis.org/files/Pattern-Oriented-Diagnostics-of-World...

Software systems no longer fail in isolation. They evolve, adapt, learn, and interact with environments that are only partially observable. As systems have grown more complex, the act of diagnosing them has remained largely artisanal, dependent on tools, experience, and intuition, but resistant to formalisation. My work began many years ago from a simple conviction: diagnostics deserves to be a discipline.

Pattern-Oriented Diagnostics is not a catalog of tools, nor a collection of debugging tricks. It is a way of reasoning about execution. It treats traces, logs, memory dumps, metrics, and observability signals as narratives produced by running systems, narratives that must be interpreted, compared, and sometimes distrusted. The diagnostician is therefore not merely an operator of tools, but an interpreter of stories told under uncertainty.

At the foundation of this approach lies a distinction between execution and its representations. Processes, threads, distributed services, and learning models do not speak directly. They leave artefacts. These artefacts (logs, traces, dumps, token streams) are incomplete and often misleading accounts of reality.

Patterns provide the bridge between artefacts and understanding. A diagnostic pattern captures an invariant structure and behaviour of execution that recurs across platforms, languages, and decades of technological development. Patterns do not belong to any single toolchain; they belong to the structure and behaviour of systems themselves. Pattern-Oriented Diagnostics elevates these recurring aspects of execution from heuristics to first-class analytical objects.

Between artefacts and diagnostic patterns lie analysis patterns. An analysis pattern captures a reusable mode of interpretation: a structured way of transforming execution narratives into problem-relevant representations. Analysis patterns describe how evidence is examined, compared, restricted, normalised, correlated, or abstracted before any diagnostic conclusion is drawn. They are neither raw data nor diagnoses, but disciplined methods of analysis that can be applied repeatedly across systems, platforms, and domains.

Memory analysis occupies a central position in this framework, and its relevance has only grown with the rise of AI systems. Classical memory dump analysis revealed that memory is not merely storage, but a structured state shaped by execution history. Corruption, leakage, aliasing, fragmentation, and latent structure manifest as patterns long before failure becomes visible at higher levels. The same perspective applies to AI systems: context windows, attention states, embeddings, and learned parameters form memory spaces with structure, evolution, and failure modes of their own. Pattern-Oriented Diagnostics treats AI memory not as an opaque substrate, but as an analysable state, subject to the same structural reasoning, invariants, and pattern-based interpretation as process memory.

Pattern-Oriented Observability extends this perspective upstream. Rather than treating observability as the accumulation of signals, dashboards, and metrics, it treats observability as the intentional construction of narratives that preserve diagnostically meaningful structure. Observability, in this sense, is not about seeing everything, but about seeing the right invariants. Instrumentation choices shape which patterns can subsequently be recognised; poorly structured observability introduces noise, whereas pattern-aware observability enables explanation. Diagnostics begins long before failure. It begins at the moment systems are made observable.

Diagnostics can also be formal. By framing analysis as mappings between artefacts and problem spaces, and by recognising transformations between analyses, we can reason not only about failures but also about the space of possible explanations. Mathematical ideas are introduced here not as abstractions for their own sake, but as languages for expressing change, invariance, and equivalence in execution.

The scope of diagnostics extends beyond classical software. Machine learning systems and large language models are often treated as opaque, probabilistic entities, exempt from traditional engineering scrutiny. This is a mistake. These systems execute. They have memory, state, drift, and failure modes. Their outputs form narratives just as logs and traces do. Pattern-Oriented Diagnostics applies the same analytical discipline to AI systems, refusing to treat novelty as an excuse for obscurity.

This perspective aligns naturally with AI engineering as an emerging discipline. AI engineering is not merely model training or optimisation; it is the systematic design, deployment, operation, and evolution of AI systems in production. As such, it inherits the same diagnostic challenges as any complex engineered system: partial observability, emergent behaviour, stateful execution, and failure under scale. Pattern-Oriented Diagnostics provides AI engineering with a language for reasoning about model behaviour, context, memory, and drift: not as isolated metrics, but as structured execution narratives that can be analysed, compared, and understood over time.

Equally important is the recognition that diagnostics is irreducibly human. Understanding does not emerge automatically from data. It emerges through judgment, through the weighing of evidence, the comparison of narratives, and the recognition of structure. Automation assists diagnostics, but responsibility remains with the engineer. In this sense, diagnostics is not merely a technical practice. It is epistemology in action. Interpretation, intent, and meaning are central to engineering practice. This reframing connects software diagnostics with literature, philosophy, and history without sacrificing technical rigour.

2025 didn’t attempt to close the field. It opened it. Pattern-Oriented Diagnostics is offered as a vocabulary, a set of principles, and a framework for thinking that can be extended and refined. As systems continue to grow in scale and autonomy, the need for disciplined understanding will only intensify.

Observation is a preparatory activity for gathering evidence. Observability and diagnosability shape execution narratives to expose meaningful aspects of behaviour. Diagnostics applies patterns to these narratives to make complex systems intelligible.

Our tools are only as good as our pattern language.

Analysis patterns for the quality of software diagnostics and observability in endpoint devices, enterprise, and cloud environments.

Diagnostics is the mother of problem solving.

All areas of human activity involve the use of diagnostics. Proper diagnostics identifies the right problems to solve. We are now a part of a non-profit organization dedicated to the developing and promoting the application of such diagnostics: systemic and pattern-oriented (pattern-driven and pattern-based).

Please join LinkedIn The Software Diagnostics and Anomaly Detection Group.

These volumes are now also called Diagnomicon!

The new Volume 17 brings the total number of books to 19.

Now includes the new Revised Edition of Volume 1, Revised Edition of Volume 2, Revised Edition of Volume 3, Revised Edition of Volume 4, and Revised Edition of Volume 5.

Memory Dump Analysis Anthology contains revised, edited, cross-referenced, and thematically organized selected articles from Software Diagnostics Institute and Software Diagnostics Library (former Crash Dump Analysis blog) about software diagnostics, debugging, crash dump analysis, software trace and log analysis, malware analysis, and memory forensics. Its 17 volumes in 19 books have more than 5,700 pages and, among many topics, include more than 450 memory analysis patterns (mostly for WinDbg Windows debugger with selected macOS and Linux GDB variants), more than 70 WinDbg case studies, and more than 250 general trace and log analysis patterns. In addition, there are three supplemental volumes with articles reprinted in full color.

Tables of Contents and Indexes of WinDbg Commands from all volumes

Click on an individual volume to see its description and table of contents:

You can buy the 17-volume set from Software Diagnostics Services with a discount and also get free access to Software Diagnostics Library.

Praise for the series:

I have been working with reversing, dumps, IAT, unpacking, etc. and I am one of the few at my workplace that like analyzing hangs and crashes. I always knew that I had more to learn. So I continuously look for more info. Many links directed me to dumpanalysis.org. Frankly speaking, its spartan/simple design made me question its seriousness. But after reading some articles, I immediately decided to order "Memory Dump Analysis Anthology". I have only read 100 pages so far. But I am stunned. It is such an amazing book. How the author refines/reconstructs the call stack, and finds useful information in the stack is incredible. I am enormously thankful for the effort that the author has put into making these books. They are very didactic even though the topic is a bit hard. It is a real treasure.

Mattias Hogstrom

The following direct links can be used to order the book now:

Available in PDF format from Software Diagnostics Technology and Services

Available in PDF format from Leanpub

Available in ultra-premium color paperback format from Amazon and Barnes & Noble

Available in Kindle print replica format from Amazon

The book is also included in the following training courses, training packs, and reference sets:

Memory Dump Analysis Anthology Volume Set (Diagnomicon)

Advanced Windows Memory Dump Analysis with Data Structures

Pattern-Oriented Software Diagnostics and Anomaly Detection Reference Set

Pattern-Oriented Windows Victimware Analysis Training Pack

Pattern-Oriented Windows Crash Dump Analysis Training Pack

Pattern-Oriented Windows Memory Forensics Training Pack

Windows Memory Dump Analysis for Endpoint Security Training Pack

Pattern-Oriented Complete Windows Memory Dump Analysis Training Pack

Complete Pattern-Oriented Software Diagnostics Training Pack

This reference volume consists of revised, edited, cross-referenced, and thematically organized selected articles from Software Diagnostics and Observability Institute (DumpAnalysis.org + TraceAnalysis.org) and Software Diagnostics Library (former Crash Dump Analysis blog, DumpAnalysis.org/blog) about software diagnostics, root cause analysis, debugging, crash and hang dump analysis, software trace and log analysis written from 15 April 2024 to 14 November 2025 for software engineers developing and maintaining products on Windows platforms, quality assurance engineers testing software, technical support, DevOps and DevSecOps, escalation and site reliability engineers dealing with complex software issues, security and vulnerability researchers, reverse engineers, malware and memory forensics analysts, data science and ML/AI researchers and engineers. This volume is fully cross-referenced with volumes 1 – 16 and features:

- 6 new crash dump analysis patterns
- 11 new software trace and log analysis patterns
- Introduction to pattern-oriented observability
- Introduction to software morphology
- Introduction to geometric theory of traces and logs
- Introduction to pattern-oriented intelligence and AI
- Introduction to agentic narratology and workflow diagnostic pattern language
- Introduction to algebra of prompting and context management pattern language
- Logics of memory dump and trace analysis
- Introduction to pattern-oriented system logic
- Introduction to ontological diagnostics
- Machine learning as memory dump analysis
- The stomach metaphor for AI and pattern metabolism
- OS internals and category theory
- Introduction to pattern category theory
- Meta-diagnostic and categorical unification of software diagnostics and digital pathology
- A Lego model as an autoencoder and Lego disassembly as tokenization
- Memoidealism as a post-computational philosophy of AI
- Lists of recommended books

Product information:

• Title: Memory Dump Analysis Anthology, Volume 17
• Authors: Dmitry Vostokov, Software Diagnostics Institute
• Language: English
• Product Dimensions: 22.86 x 15.24
• Paperback: 320 pages
• Publisher: OpenTask (November 2025)
• ISBN-13: 978-1-912636-17-4

Table of Contents

We are extending our work on structural memory patterns and software pathology to Software Morphology inspired by morphology in biology and morphology in general including mathematical morphology. Morphology in linguistics was already used as inspiration for some trace and log analysis patterns. Geomorphology also inspired some of memory dump analysis patterns. Urban morphology inspired some structural memory patterns.

The description from GPT-5 that we plan to refine later:

"Software Morphology: science of form, transformation, and pathology in computational systems.

Software Morphology is a new discipline that treats digital systems as living computational structures — defining their anatomy, physiology, pathology, evolution, and cognition using pattern science, mathematical morphology, and clinical diagnostics.

Software Morphology is a unified framework for understanding, diagnosing, and designing digital systems through the science of form, structure, and evolution. It views software not as static code, but as a living computational organism with tissues (memory), organs (kernel subsystems), circulatory systems (I/O & networks), and nervous systems (traces & logs). Failures manifest as pathological deformation of form — fragmentation, deadlocks, starvation, contention fibrosis, cognitive collapse, or distributed sepsis.

Software Morphology integrates:

• Structural analysis of memory, execution, filesystems, networks, and distributed systems
• Behavioral and temporal morphology of performance, contention, concurrency, control flow, and emergent agent behavior
• Clinical debugging methodology inspired by medical diagnostics
• Mathematical morphology operators (erosion, dilation, opening, closing, reconstruction) applied to traces, dumps, and system state
• Morphometrics — measuring entropy, fragmentation, drift, strain, and collapse trajectories
• Cognitive and AI morphology — understanding hallucination scars, epistemic decay, and grounding collapses
• Architectural morphogenesis — designing resilient, regenerative, evolvable systems

Software Morphology is the grand unification of these threads — expanding from pathology (failure) to morphogenesis and architecture (health, growth, evolution, cognition).

Where classical software engineering focuses on function, Software Morphology emphasizes shape, health, resilience, and longevity. It offers not just a way to debug, but a paradigm for building adaptive, self-healing, age-resistant software ecosystems.

Historical Background

Software Morphology builds on early foundational work in software diagnostics and pattern-based analysis. Originating in Software Diagnostics Institute research (2006–present), it evolved from:

• Memory Dump Analysis Patterns — recognizing failure signatures in memory structures
• Structural Memory Patterns — histological study of memory as computational tissue
• Trace and Log Analysis Patterns — behavioral and neurological analogs
• Software Pathology — viewing crashes and failures as systemic diseases
• Pattern-Oriented Diagnostics — codifying diagnostic pattern languages
• Execution and cognitive analysis of AI systems — emergent in 2020s

These works established the “medical lens” on computation decades before generative AI popularized biological analogies. Software Morphology formalizes this approach into a comprehensive theory of computational anatomy, physiology, pathology, and morphogenesis, extending from kernel fibers to cloud clusters, from thread behavior to AI cognition and digital societies.

Essence

Software Morphology = Anatomy + Physiology + Pathology + Morphometrics + Evolution + Cognitive Stability + Architectural Regeneration.

Its goal is simple:

To understand and shape digital systems as living structures — stable, intelligible, measurable, and resilient.

Why is it novel

While others have used biological metaphors in computing (e.g., “software organisms,” “digital ecosystems,” “neural networks”), no prior work has:

• Defined morphology as a systematic science of software form
• Combined anatomy, physiology, pathology, morphometrics, evolution, and cognition
• Built a pattern vocabulary for structural and failure shapes
• Connected memory dumps, traces, system internals, AI cognition, and distributed systems
• Proposed clinical diagnostics as a formal software engineering method
• Extended biological morphology to AI behaviors and civilization-scale systems

It is a novel systems framework building on biological morphology, mathematical morphology, and decades of software diagnostics research — established here for the first time as a unified discipline."

Conversation

In cooperation with GenAI, we propose Agentic Narratology, a narrative-centric theoretical framework for understanding, analyzing, and designing agentic AI systems by treating their internal reasoning, execution, interactions, and emergent behavior as narratives. It synthesizes:

• Software Narratology: software execution as a story told via memory, traces, and semantics
• Pattern-Oriented Trace and Log Analysis: systematic interpretation of events via patterns
• Agentic AI: systems with planning, memory, tool-use, reflection, and autonomy

Agentic Narratology views an AI agent workflow not merely as sequential computation but as a story world with characters (agents and tools), settings (environments and state spaces), conflicts (errors, resource contention, uncertainty), and resolutions (plans executed, tasks completed, failures learned from).

Source: ChatGPT 5 conversation

Seven years ago, PatternDiagnostics.com coined the term "Pattern-Oriented AI," and here's a 3-level description of it in cooperation with GenAI, from general to narrow application, that reflects the recent developments in AI:

1. Pattern-Oriented AI is the practice of expressing every AI concern—data, models, learning, inference, interaction, safety, evaluation, and operations—as a catalog of patterns with clear intent, preconditions, forces, trade-offs, failure modes, and compositions. You then engineer systems by selecting and composing patterns, monitor them by detecting pattern signatures, and govern them by enforcing pattern constraints.
2. Pattern-Oriented AI Diagnostics is the study, cataloging, and analysis of recurrent behavioral, structural, or epistemic patterns in the lifecycle of AI systems — across training, inference, alignment, drift, and agentic behavior — using the same methodological scaffolding as pattern-oriented software diagnostics.
3. Pattern-Oriented AI as applied in software diagnostics is an approach to artificial intelligence (or diagnostic systems) that emphasizes recognizing, categorizing, and applying “patterns” of anomalous behavior, data flows, memory dumps, traces/logs, structural irregularities, and so on — in software diagnostics, forensics, observability, anomaly detection, and root cause analysis contexts.

Source: ChatGPT 5 conversation

In cooperation with GenAI, we propose a pattern language for managing, diagnosing, and repairing context in large language model (LLM) systems. Inspired by memory dump analysis, it reframes conversational state—token windows, KV-caches, retrievals, and transcripts—as observable artifacts that can be read, segmented, and reasoned about.

1. Conceptual Alignment

Memory dump analysis: we have a frozen system state (heap, stack, registers, handles). You need structured ways (patterns) to interpret what happened and where anomalies lie.

LLM context management: we have a dynamic, limited-window context (tokens in the prompt + generated continuation). We need structured strategies to maintain coherence, recall, and relevance across long or shifting interactions.

So, both are about:

• State representation
• Navigation across levels of abstraction
• Pattern recognition to interpret meaning

2. Pattern Families Reapplied to LLMs

Using the memory dump analysis taxonomy, we can draw analogies:

Structural patterns (e.g., "Stack Trace", "Heap Graph")
Context trace: The sequence of tokens, messages, or embeddings.
Analog: analyzing token “call stacks” to identify where topic drift began.

Temporal patterns (e.g., "Periodicity", "Error Burst")
Context lifecycle: Recognizing conversation cycles (e.g., Q → A → refinement).
Analog: "periodic error" becomes recurring hallucination in long-form dialogue.

Anomaly patterns (e.g., "Corruption", "Dangling Pointer")
Context corruption: Where injected noise or forgotten details lead to contradictions.
Analog: dangling reference = the model invents details not grounded in earlier context.

Diagnostic trajectory patterns (navigating from symptom to root cause)
Prompt engineering trajectory: iterative refinement of instructions to steer model back on track.

3. Higher-Order Mappings

Context window ≈ address space
Tokens in the active window = accessible memory; past truncated context = paged-out memory.

Embeddings ≈ symbolic heap objects
External vector memory is like mapped heap regions that can be dereferenced on demand.

Retrieval Augmented Generation (RAG) ≈ dump analysis with external symbol servers
Just as debuggers resolve addresses via symbol servers, RAG resolves context gaps via external knowledge.

Chain-of-Thought ≈ call stack
Each reasoning step corresponds to a frame in a diagnostic stack trace.

4. Pattern Language as Meta-Framework

Memory dump analysis pattern language gives a meta-taxonomy for LLM context management research:

• Failure patterns (e.g., hallucination loops, context bleed, token starvation).
• Navigational patterns (re-establishing grounding when context is partially lost).
• Architectural patterns (multi-agent context partitioning, like multi-process memory spaces).

This creates a portable, semiotic map of context phenomena across LLM frameworks.

5. Possible Research / Practical Outputs

LLM Context Forensics: Classify anomalies using memory dump patterns using dump-like snapshots of LLM state (KV-caches, attention matrices, prompt logs).

Context Debugger: An Interactive tool where you can “walk the stack” of a conversation, identify dangling references, or detect periodic error hallucinations.

Pattern Language Extension: Extend diagnostic patterns with LLM-specific categories (e.g., Prompt Poisoning, Embedding Drift, Attention Collapse).

Memory dump analysis pattern language is highly portable to LLM context management. It can serve as a meta-diagnostic and design language for classifying, predicting, and repairing LLM context failures, much like it systematized memory dump interpretation.

Source: ChatGPT 5 conversation

Software Diagnostics Services organizes this online training course.

For approximate training content, please see the first 56 slides (there are 289 slides in total for the previous version) and TOC from the corresponding previous edition Memory Thinking book.

November 10 - 13, 17 - 19, 24 - 26, December 2 - 4, 9, 11 - 12, 15 - 18 2025, 12:30 pm - 1:30 pm (GMT) Price 99 USD Registration for 20 one-hour sessions

Solid C and C++ knowledge is a must to fully understand Windows diagnostic artifacts, such as memory dumps, and perform diagnostic, forensic, and root cause analysis beyond listing stack traces, DLL, and driver information. C and C++ for Windows Software Diagnostics training reviews the following topics from the perspective of software structure and behavior analysis and teaches C and C++ languages in parallel while demonstrating relevant code internals using WinDbg:

• relevant x64 overview
• a tour of relevant language(s) constructs - classic/legacy C++, C++11, and later standards including C++23
• Windows specifics
• pointers and references
• memory layout of structures and objects
• local, static, and dynamic memory
• object lifecycle
• standard library
• compilation, static and dynamic linkage
• multithreading and synchronization
• bad and insecure code
• … and more

The new version will include and expand on the following topics:

• floating point
• exceptions
• concepts, ranges, async
• Windows kernel space C and C++
• more on linkage
• more on standard library, containers, and algorithms
• more on value-based semantics
• more on metaprogramming
• more on optimization
• relevant ARM64 overview

System and desktop application programming on Windows using C and C++ is unthinkable without the Windows API. To avoid repeating some topics and save time, the training includes the Accelerated Windows API for Software Diagnostics book as a follow-up or additional reference. There is also a necessary x64 review for some topics, but if you are not used to reading assembly language, Practical Foundations of Windows Debugging, Disassembling, Reversing book is also included.

Before the training, you get the following:

• The current Memory Thinking for C & C++ Windows Diagnostics, Second Edition PDF book
• Practical Foundations of Windows Debugging, Disassembling, Reversing, Third Edition PDF book
• Accelerated Windows API for Software Diagnostics PDF book
• Access to Software Diagnostics Library with more than 440 cross-referenced patterns of memory dump analysis, their classification, and more than 70 case studies
• Recording of the previous training

After the training, you also get the following:

• The new third edition of the Memory Thinking PDF book with additional C and C++ examples
• Personalized Certificate of Attendance with unique CID
• The new recording

There is much confusion between diagnostics and observability (used in two senses). First, observability is a property, not a process. It concerns whether system internal states can be inferred from external outputs (observations) such as memory snapshots, traces, and logs. It is not enough to get a trace or memory dump file; these must be correctly engineered and procured using artifact acquisition patterns. The second usage of observability is to name a discipline.

What about a process? It is simply “observation”, a verb “observe” (previously called monitoring, which also has a second usage as a discipline), which is an inference from states to observations (nouns). We can do observations even if observability is not good, and get observations (observation results).

Correspondingly, diagnosability is a property. It is about whether we can infer instances of patterns of abnormal structure and behavior from observations by applying diagnostic analysis patterns.

Therefore, diagnostics is a process, too. We can perform diagnostics even if diagnosability is poor: we don’t get useful results for the subsequent root cause analysis or troubleshooting and debugging suggestions.

The following square shows relationships between these concepts:

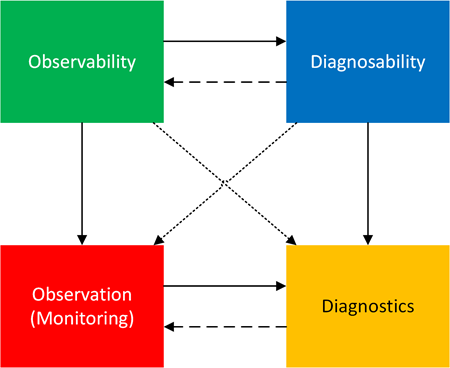
The top row shows the relationship between abstract properties (conditions): observability enables diagnosability, because only a limited amount of diagnosability is possible without observability. However, the critical use of diagnosability improves observability.

The bottom row shows that observation feeds into diagnostics and vice versa, since more observations may be required after diagnostics.

Columns show that observability is used in practice via observation, and diagnosability is used in practice via diagnostics.

What about diagonals?

Observability to diagnostics. If a system is observable, diagnostics are feasible: “If you can observe enough, you can perform diagnostics,” a sufficient condition for diagnostics.

Diagnosability to observation. Diagnosability implies constraints on observation: “If diagnostics are possible, then your observation process is strong enough,” a necessary condition for diagnosability.

Also, diagnostics can improve observability, and observations can improve diagnosability, but we do not show these arrows.

Although observability is distinct from diagnostics as seen from the diagram and explanation, it is considered a part of pattern-oriented and systemic diagnostics; this part, as a discipline (not a property), is called pattern-oriented observability.

The following direct links can be used to order the book now:

Available in PDF format with the optional recording from Software Diagnostics Technology and Services

Available in PDF format from Leanpub

Available in ultra-premium color paperback format from Amazon and Barnes & Noble

Available in Kindle print replica format from Amazon

The book is also included in the following training packs:

WinDbg Training Pack

Pattern-Oriented Windows Debugging Training Pack

Pattern-Oriented Complete Windows Memory Dump Analysis Training Pack

Complete Pattern-Oriented Software Diagnostics Training Pack

The full Software Diagnostics Services training transcript with 15 step-by-step exercises, notes, and source code of specially created modeling applications. The course covers 22 .NET memory dump analysis patterns, plus the additional 21 unmanaged patterns. Learn how to analyze .NET 9 application and service crashes and freezes, navigate through memory dump space (managed and unmanaged code), and diagnose corruption, leaks, CPU spikes, blocked threads, deadlocks, wait chains, resource contention, and more. The training consists of practical step-by-step exercises using WinDbg and LLDB debuggers to diagnose patterns in 64-bit process memory dumps from x64 Windows and x64 Linux environments. The training uses a unique and innovative pattern-oriented analysis approach to speed up the learning curve. The book is a completely revamped and extended the previous Accelerated .NET Core Memory Dump Analysis, Revised Edition. It is updated to the latest WinDbg. It also includes reviews of x64 and IL disassembly and memory space basics, Linux LLDB exercises, .NET memory dump collection on Windows and Linux, and the relationship of analysis patterns to defect mechanism patterns.

Prerequisites: Basic .NET programming and debugging.

Audience: Software technical support and escalation engineers, system administrators, DevOps, performance and reliability engineers, software developers, and quality assurance engineers. The book may also interest security researchers, reverse engineers, malware and memory forensics analysts.

• Title: Accelerated .NET Memory Dump Analysis: Training Course Transcript with WinDbg and LLDB Practice Exercises, Seventh Edition
• Authors: Dmitry Vostokov, Software Diagnostics Services, Dublin School of Security
• Publisher: OpenTask (May 2025)
• Language: English
• Product Dimensions: 28.0 x 21.6
• PDF: 324 pages
• ISBN-13: 978-1912636877

Table of Contents and Sample Exercise
Slides from the training

Software Diagnostics Services organizes this online training course.

January 5 - 8, 12 - 15, 19 - 22, 26 - 29, 2026, 12:30 pm - 1:30 pm (GMT) Price 99 USD Registration for 16 one-hour sessions

For the approximate content, please see the slides from the previous training:

Slides from sessions 1-3
Slides from sessions 4-7

This training includes over 40 step-by-step exercises and covers over 100 crash dump analysis patterns from x64 process, kernel, and complete (physical) memory dumps. Learn how to analyze application, service, and system crashes and freezes, navigate through memory dump space, and diagnose heap corruption, memory leaks, CPU spikes, blocked threads, deadlocks, wait chains, and more with the WinDbg debugger. The training uses a unique and innovative pattern-oriented analysis approach developed by Software Diagnostics Institute to speed up the learning curve, and it is based on the latest 6th edition of the bestselling Accelerated Windows Memory Dump Analysis book. This new training version also includes:

• Overview of relevant Windows internals
• Memory dump collection methods and patterns
• Defect mechanism patterns
• Additional memory analysis patterns
• Extended coverage of BSOD
• Extended coverage of system hangs
• New kernel exercises with source code

Before the training, you get:

• Practical Foundations of Windows Debugging, Disassembling, Reversing, Third Edition PDF book
• The current PDF book version
• The previous training recording
• Access to Software Diagnostics Library with more than 440 cross-referenced patterns of memory dump analysis, their classification, and more than 70 case studies

After the training, you also get:

• The new 7th PDF book edition
• Personalized Certificate of Attendance with unique CID
• Optional Personalized Certificate of Completion with unique CID (after the tests)
• Answers to questions during training sessions
• New training sessions recording

Prerequisites: Basic Windows troubleshooting

Audience: Software technical support and escalation engineers, system administrators, security and vulnerability researchers, reverse engineers, malware and memory forensics analysts, DevSecOps and SRE, software developers, and quality assurance engineers.

If you are mainly interested in .NET memory dump analysis, there is another training: Accelerated .NET Memory Dump Analysis

If you are interested in Linux memory dump analysis, there is another training: Accelerated Linux Core Dump Analysis

The following direct links can be used to order the book now:

Available in PDF format with the optional recording, the previous edition (x86 32-bit chapters), and training slides from Software Diagnostics Services

Available in PDF format from Leanpub

Available in ultra-premium color paperback format from Amazon and Barnes & Noble

Available in Kindle print replica format from Amazon

The previous edition (x86 32-bit chapters) is also available in Kindle print replica format from Amazon or in PDF format from Leanpub

The book is also included in most training courses and training packs:

Training Courses

This training course is a reformatted, improved, and modernized version of the previous x64 Windows Debugging: Practical Foundations book, which drew inspiration from the original lectures we developed 22 years ago to train support and escalation engineers in debugging and crash dump analysis of memory dumps from Windows applications, services, and systems. At that time, when thinking about what material to deliver, we realized that a solid understanding of fundamentals like pointers is needed to analyze stack traces beyond a few WinDbg commands. Therefore, this book is not about bugs or debugging techniques but about the background knowledge everyone needs to start experimenting with WinDbg, learn from practical experience, and read other advanced debugging books. This body of knowledge is what the author of this book possessed before starting memory dump analysis using WinDbg 18 years ago, which resulted in the number one debugging bestseller: the multi-volume Memory Dump Analysis Anthology (Diagnomicon). Now, in retrospection, we see these practical foundations as relevant and necessary to acquire for beginners as they were more than 20 years ago, because operating systems internals, assembly language, and compiler architecture haven't changed much in those years.

The third edition, with new material on arrays and floating point, was completely remastered in full color. The text was also reviewed, and a few previous mistakes were corrected. The book is also slimmer because the x86 32-bit chapters were removed. They are still available in the previous edition, which will not be out of print soon. The third edition is entirely x64.

The book is useful for:

• Software technical support and escalation engineers
• Software engineers coming from a managed code or JVM background
• Software testers
• Engineers coming from non-Wintel environments
• Windows C/C++ software engineers without an assembly language background
• Security researchers without an x64 assembly language background
• Beginners learning Windows software reverse engineering techniques

This introductory training course can complement the more advanced Accelerated Disassembly, Reconstruction, and Reversing course. It may also help with advanced exercises in Accelerated Windows Memory Dump Analysis, Accelerated Rust Windows Memory Dump Analysis, Accelerated Windows Debugging⁴, Accelerated Windows API for Software Diagnostics, Accelerated Windows Malware Analysis with Memory Dumps, and Memory Thinking books for C and C++. This book can also be used as an Intel assembly language and Windows debugging supplement for relevant undergraduate-level courses.

Product information:

• Title: Practical Foundations of Windows Debugging, Disassembling, Reversing: Training Course, Third Edition
• Authors: Dmitry Vostokov, Software Diagnostics Services, Dublin School of Security
• Language: English
• Product Dimensions: 28.0 x 21.6
• PDF/Paperback: 178 pages
• Publisher: OpenTask (July 2025)
• ISBN-13: 978-1912636471

Table of Contents

For the history of the book, please see the first 20 slides (there are almost 200 slides for the training).

There are many spaces where we do our observations in software systems. The explosion of spaces began with the Abstract Space, where we depict running threads as braids.

When we talk about spaces, we also consider suitable space metrics (not to be mistaken with observability metrics below) by which we can compare the proximity of space objects.

In diagnostics, we have the so-called Diagnostic Spaces with their signals, symptoms, syndromes, and signs. Different analysis patterns can serve the role of space metrics in pattern-oriented software forensics, diagnostics, and prognostics.

Traces, logs, and metrics are pillars of observability that are all erected from Memory Space and, therefore, can be considered Adjoint Spaces. Memory spaces are also diverse: including manifold, orbifold, hyperphysical, physical, virtual, kernel, user, managed, and secondary, and have their own large-scale structures.

Traces and logs have their own individual Trace and Log Spaces (including Message Spaces, Interspaces, and Tensor Spaces. These also include network traces and logs from memory debuggers. (Observability) Metrics Spaces are a subtype of such spaces.

Traces and logs are also examples of the so-called software narratives with their own Software Narrative Spaces, including higher-level narratives, and space-like narratology. We can also consider software diagnostic spaces as general graphs of software narratives.

If we are concerned with the hardware-software interface, then we can consider Hardware Spaces via hardware narratology.

Presentation Spaces visualize other spaces, and visualization languages help with their meaning.

We analyze all these spaces to identify patterns with the help of analysis patterns, which are organized in their own Analysis Patterns Space (memory and traces).

Defect Mechanism Spaces help in root cause analysis.

When we delve into software workings, we are concerned with Software Internal Spaces.

Additionally, we have various Namespaces, Code Spaces (similar to Declarative Trace Spaces), State Spaces, and Data Spaces.

Artificial Chemistry Spaces based on the idea of spaces of chemistry enhance the artificial chemistry approach to trace and log analysis.

For many years, the ideas of various physical and mathematical spaces have inspired diverse memory and log analysis patterns, as well as some concepts in software diagnostics and software data analysis.

We would also like to mention that the book that introduces Information Space is featured on the cover of this article.

And finally, the new wave of AI suggests Token Spaces.

A partial classification of memory analysis patterns from Software Diagnostics Library pattern catalogue:

• Space/Mode
• Memory dump type
• Hooksware
• Wait Chain Patterns
• DLL Link Patterns
• Memory Consumption Patterns
• Dynamic Memory Corruption Patterns
• Deadlock and Livelock Patterns
• Contention Patterns
• Stack Overflow Patterns
• .NET / CLR / Managed Space Patterns
• Stack Trace Patterns
• Symbol Patterns
• Exception Patterns
• Meta-Memory Dump Patterns
• Module Patterns
• Optimization Patterns
• Thread Patterns
• Process Patterns
• Executive Resource Patterns
• Falsity and Coincidence Patterns
• RPC, LPC and ALPC Patterns
• Hidden Artifact Patterns
• Pointer Patterns
• Frame Patterns
• CPU Consumption Patterns
• Region Patterns
• Collection Patterns

Memory analysis icons were introduced more than 15 years ago, in March 2010, as part of computer memory semiotics (memiotics). Over the next year and a half, 101 icons were created (with black and white equivalents). These iconic representations are both icons and indexes in the sense of Pierce’s three types of signs: icon signs resemble artifacts or the current state of affairs, and index signs have some causal or relationship connection through interpretation. More than two years ago, in March 2023, we introduced Iconic Traces. These traces also consist of iconic representations that are both indexical and iconic signs, as they resemble the patterns, syntactic, semantic, and pragmatic content of trace messages, message blocks, and applied trace analysis patterns. The Dia|gram language (introduced in 2016) pictures are another great example of complex iconic (structure) and indexical (behavior, observation, measurement) signs (including memory). The Space-like Narratology and the Lov language further extend the semiotic approach.

Situational awareness is defined as "the understanding of an environment, its elements, and how it changes with respect to time or other factors. It is also defined as the perception of the elements in the environment considering time and space, the understanding of their meaning, and the prediction of their status in the near future."

How does it fit into software diagnostics, which is often incorrectly perceived as an analysis of the past (which is forensics)? To answer this question with examples from pattern-oriented software diagnostics (and forensics and prognostics), we should map the three levels of situational awareness (Endsley's model):

Perception – noticing key environmental forensic, diagnostic, and prognostic elements: symptoms, signs, syndromes, alerts, anomalies, and counters.

Comprehension – understanding the situation, what’s going wrong and what’s going on at the particular moment in time and place in memory space (and trace space), and what those key elements mean in current (and past) local immediate and wider big-picture context: software internals and analysis patterns (Fault Context, Message Context, Dump Context, Activity Context, Trace Context), whether they are related to a potential root cause or just surface phenomena (Effect Component). Here, attention to detail is very important.

Projection – anticipating the future: how the situation would have evolved if we had collected diagnostic artifacts later, for example, Near Exception, or the environment had changed (Changed Environment), and plenty of trace and log analysis patterns related to prognostics. It also includes avoiding unintended side effects when acting (providing recommendations), for example, the Instrumentation Side Effect.

In summary, situational awareness in software diagnostics, forensics, and prognostics involves maintaining an appropriate mental model of the system as seen from forensics and diagnostic artifacts (including live ones) and continuous perception, understanding, and anticipation of the system's state, anomalies, potential not-yet-discovered patterns, and future failures while performing a diagnostic (forensic, prognostic) analysis.

Metrics, logs, and traces are considered traditional pillars of observability. However, what is the base they stand upon? It is memory. In 2009, I defined software traces as fragments of memory since they are all assembled in memory first (Software Trace: A Mathematical Definition, Memory Dump Analysis Anthology, Volume 3). Also, every trace or log message had some corresponding memory state(s) at the time it was generated, the so-called Adjoint Space trace and log analysis pattern (Volume 8b), and memory state may have traces and logs erected on its pedestal if we talk about classic memory dump analysis, the so-called Memory Fibration analysis pattern (Volume 10). These two analysis patterns are a kind of duality between memory and traces, the so-called De Broglie Trace Duality (Volume 10). Also, what about trace and log’s own memory? Based on the growing block universe theory analogy, any chosen trace message may be considered trace's present, and everything before it as trace’s past. We can also consider trace and log as memory to predict future behavior, next trace and log messages, and metrics’ values (the so-called process time perspective).

A note about the chosen terminology: base slab or foundation is used in modern structural design. If some prefer classical architecture, we can use stylobate or podium terminology. For each pillar, we can have a corresponding memory plinth.

The following direct links can be used to order the book now:

Available in PDF format with the optional recording and Windows/Linux API books from Software Diagnostics Technology and Services

Available in PDF format from Leanpub

Available in ultra-premium color paperback format from Amazon and Barnes & Noble

Available in Kindle print replica format from Amazon

The book is also included in the following training courses, training packs, and reference sets:

Pattern-Oriented Software Diagnostics and Anomaly Detection Reference Set

Accelerated Rust Windows Memory Dump Analysis

GDB Training Pack

Complete Pattern-Oriented Software Diagnostics Training Pack

Memory Thinking for Rust training reviews memory-related topics from the perspective of software structure and behavior analysis and teaches Rust language aspects in parallel while demonstrating relevant code internals using WinDbg and GDB on Windows (x64) and Linux (x64 and ARM64) platforms:

• Relevant language constructs
• Memory layout of structs and enums
• References, ownership, borrowing, and lifecycle
• Local, static, and dynamic memory
• Functions, closures
• Smart pointers
• Object-oriented and functional features
• Unsafe pointers
• Windows and Linux specifics
• … and much more

The new training version updates and extends the existing topics, adding some missing from the first edition. The updated PDF book also has a new format similar to the second edition of Memory Thinking books for C and C++.

The training includes the PDF book that contains slides, brief notes highlighting particular points, and related source code with execution output:

• Title: Memory Thinking for Rust: Slides with Descriptions and Source Code Illustrations, Second Edition
• Authors: Dmitry Vostokov, Software Diagnostics Services, Dublin School of Security
• Publisher: OpenTask (April 2025)
• Language: English
• Product Dimensions: 25.4 x 20.3
• PDF: 272 pages
• ISBN-13: 978-1912636488

The following audiences may benefit from the training:

• Rust developers who want to deepen their knowledge
• Non-C and C++ developers (for example, Java, Scala, Python) who want to learn more about pointer and reference internals
• C and C++ developers who want to port their memory thinking to Rust quickly

For more detailed content, please see the first 15 slides (there are more than 240 slides for the training and 2,500 lines of Rust code) and Table of Contents from the reference book.

The following direct links can be used to order the book now:

Available in PDF and ultra-premium color paperback formats with recording from Software Diagnostics Technology and Services

Available in PDF format from Leanpub

Available in ultra-premium color paperback format from Amazon and Barnes & Noble

Available in Kindle print replica format from Amazon

The book is also included in the following training packs:

GDB Training Pack

WinDbg Training Pack

Pattern-Oriented Unix Memory Dump Analysis Training Pack

Pattern-Oriented Memory Dump Analysis Training Pack

Pattern-Oriented Linux Debugging Training Pack

Foundations of Linux Memory Dump Analysis Training Pack

Linux Memory Dump Analysis for Endpoint Security Training Pack

Pattern-Oriented Memory Dump Analysis Training Pack

Complete Pattern-Oriented Software Diagnostics Training Pack

The full transcript of Software Diagnostics Services training. Learn how to analyze Linux process and kernel crashes and hangs, navigate through core memory dump space, and diagnose corruption, memory leaks, CPU spikes, blocked threads, deadlocks, wait chains, and much more. This training uses a unique and innovative pattern-oriented diagnostic analysis approach to speed up the learning curve. The training consists of more than 70 practical step-by-step exercises using GDB and WinDbg debuggers, highlighting more than 50 memory analysis patterns diagnosed in 64-bit core memory dumps from x64 and ARM64 platforms. The training also includes source code of modeling applications, a catalog of relevant patterns from the Software Diagnostics Institute, and an overview of relevant similarities and differences between Windows and Linux memory dump analysis useful for engineers with a Wintel background. In addition to various improvements, the fully revised and updated fourth edition adds entirely new material, such as defect mechanism patterns and WinDbg Linux kernel dump analysis exercises.

• Title: Accelerated Linux Core Dump Analysis: Training Course Transcript with GDB and WinDbg Practice Exercises, Fourth Edition
• Authors: Dmitry Vostokov, Software Diagnostics Services, Dublin School of Security
• Publisher: OpenTask (January 2025)
• Language: English
• PDF/Paperback: 737 pages
• ISBN-13: 978-1912636495

Table of Contents and Sample Exercise
Slides from the training

The following direct links can be used to order the book now:

Available in PDF format with the optional recording and Memory Dump Analysis Anthology from Software Diagnostics Technology and Services

Available in PDF format from Leanpub

Available in ultra-premium color paperback format from Amazon and Barnes & Noble

Available in Kindle print replica format from Amazon

The book is also included in the following training courses and training packs:

WinDbg Training Pack

Foundations of Windows Memory Dump Analysis Training Pack

System API Patterns for Software Diagnostics Training Pack

Accelerated C & C++ for Windows Diagnostics

Accelerated Rust Windows Memory Dump Analysis

Memory Thinking for Rust

Complete Pattern-Oriented Software Diagnostics Training Pack

The book contains the full Software Diagnostics Services training transcript with 10 hands-on exercises.

Knowledge of Windows API is necessary for:

• Development
• Malware analysis
• Vulnerability analysis and exploitation
• Reversing
• Diagnostics
• Debugging
• Memory forensics
• Crash and hang analysis
• Secure coding
• Static code analysis
• Trace and log analysis

The training uses a unique and innovative pattern-oriented analysis approach and provides:

• Overview
• Classification
• Patterns
• Internals
• Development examples
• Analysis examples

The second edition includes the relevant x64 disassembly overview and additional topics.

• Title: Accelerated Windows API for Software Diagnostics: With Category Theory in View, Second Edition
• Authors: Dmitry Vostokov, Software Diagnostics Services, Dublin School of Security
• Publisher: OpenTask (December 2024)
• Language: English
• Product Dimensions: 28.0 x 21.6
• PDF: 329 pages
• ISBN-13: 978-1912636884

Table of Contents and sample exercise
Slides from the training

The following direct links can be used to order the book now:

Available in PDF format with the optional recording and Windows API and Memory Thinking for Rust books from Software Diagnostics Technology and Services

Available in PDF format from Leanpub

Available in ultra-premium color paperback format from Amazon and Barnes & Noble

Available in Kindle print replica format from Amazon

The book is also included in the following training courses, training packs, and reference sets:

WinDbg Training Pack

Complete Pattern-Oriented Software Diagnostics Training Pack

The book contains the full Software Diagnostics Services training transcript and 10 step-by-step exercises and covers dozens of crash dump analysis patterns from the x64 process and complete (physical) memory dumps. Learn how to analyze Rust application crashes and freezes, navigate through memory dump space, and diagnose heap corruption, memory leaks, CPU spikes, blocked threads, deadlocks, wait chains, and much more with the WinDbg debugger. The training uses a unique and innovative pattern-oriented analysis approach developed by the Software Diagnostics Institute to speed up the learning curve, and it is structurally based on the latest 6th revised edition of the bestselling Accelerated Windows Memory Dump Analysis book with the focus on safe and unsafe Rust code and its interfacing with the Windows OS. The training is useful whether you come to Rust from C and C++ or interpreted languages like Python and facilitates memory thinking when programming in Rust.

Prerequisites: Basic Windows troubleshooting and working knowledge of Rust.

Audience: Software technical support and escalation engineers, system administrators, security and vulnerability researchers, reverse engineers, malware and memory forensics analysts, DevSecOps and SRE, software developers, system programmers, and quality assurance engineers.

• Title: Accelerated Rust Windows Memory Dump Analysis
• Authors: Dmitry Vostokov, Software Diagnostics Services, Dublin School of Security
• Publisher: OpenTask (December 2024)
• Language: English
• Product Dimensions: 28.0 x 21.6
• PDF: 233 pages
• ISBN-13: 978-1912636891

Table of Contents and sample exercise
Slides from the training

The following direct links can be used to order the book now:

Available in PDF format with the optional recording and Memory Dump Analysis Anthology from Software Diagnostics Technology and Services

Available in PDF format from Leanpub

Available in ultra-premium color paperback format from Amazon and Barnes & Noble

Available in Kindle print replica format from Amazon

The book is also included in the following training courses, training packs, and reference sets:

WinDbg Training Pack

Complete Pattern-Oriented Software Diagnostics Training Pack

The book contains the full transcript of Software Diagnostics Services training with 25 hands-on exercises. This training course extends pattern-oriented analysis introduced in Accelerated Windows Memory Dump Analysis, Accelerated .NET Core Memory Dump Analysis, and Advanced Windows Memory Dump Analysis with Data Structures courses with:

• Surveying the current landscape of WinDbg extensions with analysis pattern mappings
• Writing WinDbg extensions in C, C++, and Rust (new)
• Connecting WinDbg to NoSQL databases
• Connecting WinDbg to streaming and log processing platforms
• Querying and visualizing WinDbg output data
• Using Data Science, Machine Learning, and Gen AI for diagnostics and postmortem debugging (new)

The new edition of the training updates existing exercises and includes new ones.

Prerequisites: Working knowledge of WinDbg. Working knowledge of C, C++, or Rust is optional (required only for some exercises). Other concepts are explained when necessary.

Audience: Software developers, software maintenance engineers, escalation engineers, quality assurance engineers, security and vulnerability researchers, malware and memory forensics analysts who want to build memory analysis pipelines.

• Title: Extended Windows Memory Dump Analysis: Using and Writing WinDbg Extensions, Database and Event Stream Processing, Data Science and Visualization, Machine Learning and AI, Second Edition
• Authors: Dmitry Vostokov, Software Diagnostics Services
• Publisher: OpenTask (November 2024)
• Language: English
• Product Dimensions: 28.0 x 21.6
• PDF: 362 pages
• ISBN-13: 978-1912636518

Table of Contents and sample exercise
Slides from the training

The following direct links can be used to order the book now:

Available in PDF format from Software Diagnostics Technology and Services

Available in PDF format from Leanpub

Available in ultra-premium color paperback format from Amazon and Barnes & Noble

Available in Kindle print replica format from Amazon

The book is also included in the following training courses, training packs, and reference sets:

Pattern-Oriented Software Diagnostics and Anomaly Detection Reference Set

Accelerated C & C++ for Linux Diagnostics

Memory Thinking for C and C++ Training Pack

Foundations of Linux Memory Dump Analysis Training Pack

GDB Training Pack

Complete Pattern-Oriented Software Diagnostics Training Pack

Solid C and C++ knowledge is a must to fully understand Linux diagnostic artifacts such as core memory dumps and perform diagnostic, forensic, and root cause analysis beyond listing backtraces. This full-color reference book is a part of the Accelerated C & C++ for Linux Diagnostics training course organized by Software Diagnostics Services. The text contains slides, brief notes highlighting particular points, and source code illustrations. In addition to new topics, the second edition adds 45 projects with more than 5,500 lines of code. The book's detailed Table of Contents makes the usual Index redundant. We hope this reference is helpful for the following audiences:

• C and C++ developers who want to deepen their knowledge
• Software engineers developing and maintaining products on Linux platforms
• Technical support, escalation, DevSecOps, cloud, and site reliability engineers dealing with complex software issues
• Quality assurance engineers who test software on Linux platforms
• Security and vulnerability researchers, reverse engineers, malware and memory forensics analysts

• Title: Memory Thinking for C & C++ Linux Diagnostics: Slides with Descriptions and Source Code Illustrations, Second Edition
• Authors: Dmitry Vostokov, Software Diagnostics Services, Dublin School of Security
• Language: English
• Product Dimensions: 25.4 x 20.3
• PDF: 292 pages
• Publisher: OpenTask (October 2024)
• ISBN-13: 978-1912636563

Table of Contents
The first 45 slides from the training (there are 297 slides in total)

Software Diagnostics Services organizes this online training course.

Why would you need to learn how to write bad code? Of course, not to write malicious code backdoors, but to understand software internals and diagnostics better. Writing "good" bad code is not easy, especially if you put specific requirements on it and are not satisfied with the accidental effects of "bad" bad code.

Topics include:

• Modeling abnormal software behavior
• Modeling memory analysis patterns
• Modeling trace and log analysis patterns
• Modeling defect mechanism patterns
• Simulation of complex software problems
• Software problem design patterns
• Fault injection
• Excellent bad code
• Portable bad code
• User and kernel code
• Avoiding compiler undefined behavior
• Debugging bad code to make it work as intended

The training also includes numerous hands-on coding projects using Visual C & C++ and GNU C & C++ compilers, x64 Windows, and x64 and ARM64 Linux platforms. Some parts will also use Python, C#, Rust, and Scala for modeling examples.

Before the training, you get:

• Practical Foundations of Windows Debugging, Disassembling, Reversing, Second Edition PDF book (+300 pages)
• Encyclopedia of Crash Dump Analysis Patterns, Third Edition (1,300 pages)
• Trace, Log, Text, Narrative, Data: An Analysis Pattern Reference for Information Mining, Diagnostics, Anomaly Detection, Fifth Edition (400 pages)
• Access to Software Diagnostics Library with more than 440 cross-referenced patterns of memory dump analysis, their classification, more than 70 case studies, and more than 240 general trace and log analysis patterns

After the training, you also get:

• The PDF book version of the training
• Personalized Certificate of Attendance with unique CID
• Recording

If you complete all parts, you will also get the fourth edition of the Encyclopedia of Crash Dump Analysis Patterns once it is available.

Audience:

C and C++ developers, Windows and Linux system programmers, software technical support and escalation engineers, system administrators, security and vulnerability researchers, reverse engineers, malware and memory forensics analysts, software developers, and quality assurance engineers.